1. 相关性度量

为了定量的描述线性相关性，统计学奠基人K. Pearson提出了Pearson相关系数、心理学家CE. Spearman提出了Spearman等级相关系数、统计学家M. Kendall提出了Kendall秩相关系数。这三种相关系数最具有代表性、应用也最广泛，它们既有联系又有不同，分别有不同的适用场景。

Pearson相关系数

Pearson相关系数 (Pearson correlation coefficient)用于度量两个变量X、Y的相关性（线性相关），定义如下：

\[ r = \frac{\sum_{i=1}^n (X_i - \overline{X}) (Y_i - \overline{Y})}{\sqrt{\sum_{i}(X_i - \overline{X})^2} \sqrt{\sum_{i}(Y_i - \overline{Y})^2}} \]

容易证明Pearson相关系数的取值范围为[-1, 1]。

• 若为1意味着X和Y的数据点基本落在一条直线上，且Y随X的增加而增加，换言之X和Y可以由直线方程来描述（线性正相关）；
• 若为-1则表示X和Y线性负相关，Y随X的增加而减少；
• 若为0，则说明二者没有线性关系。

下图给出了当Pearson相关系数为不同值时X和Y的散点图（以下三张图片均来自于Wikipedia）：

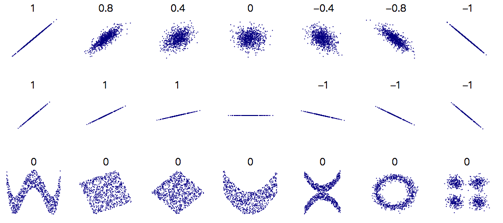
Pearson相关系数有一个重要的数学特性是，因两个变量的位置和尺度的变化并不会引起该系数的改变，即它该变化的不变量 (由符号确定)。也就是说，我们如果把X移动到a + bX和把Y移动到c + dY，其中a、b、c和d是常数，并不会改变两个变量的相关系数（该结论在总体和样本Pearson相关系数中都成立）。

Spearman相关系数

Spearman相关系数实际上就是将变量X和Y替换成其对应等级x, y的Pearson相关系数：

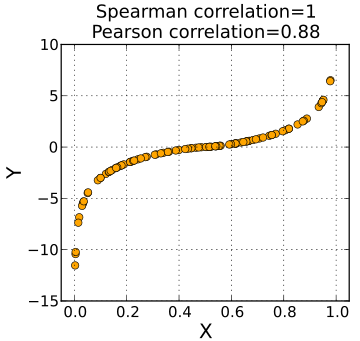
\[ \rho = \frac{\sum_{i=1} (x_i - \overline{x}) (y_i - \overline{y})}{\sqrt{\sum_{i}(x_i - \overline{x})^2} \sqrt{\sum_{i}(y_i - \overline{y})^2}} \]

相较于Pearson相关系数，Spearman相关系数更能描述两个变量之间的单调性的相关性，对于样本中的显著离群点更为不敏感。比如，下图中变量X和Y的Pearson相关系数、Spearman相关系数分别为0.88与1，显然Spearman相关系数更好地刻画了两个变量增长趋势的相关性。

下图更好地表现出了Spearman相关系数的抗噪音性：

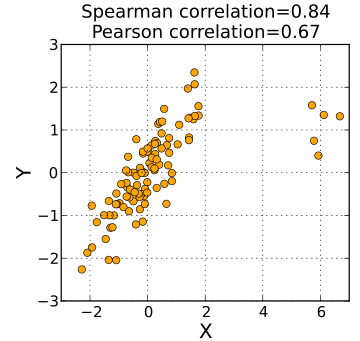
Kendall相关系数

Kendall相关系数是另一种等级相关统计量，其主要思想是根据两个变量序对的一致性 (concordance)来判断相关性的。一致性序对 (concordant pair)定义如下：如果变量对\((X_i, Y_i)\)、\((X_j, Y_j)\)且\(i \neq j\)满足当\(X_i < X_j\)时\(Y_i < Y_j\)，或者当\(X_i > X_j\)时\(Y_i > Y_j\)。反之，则为非一致性序对。那么，Kendall相关系数的定义如下：

\[ \tau = \frac{P - Q}{n(n-1)/2} \]

其中，\(P\)为一致性序对的个数，\(Q\)为非一致性序对个数，则\(P + Q = n(n-1/2)\)，因此上式可改写为

\[ \tau = \frac{4P}{n(n-1)/2} -1 \]

显然\(\tau\)的取值范围为[-1, 1]，

• 当等于1时，表示两个变量拥有一致的等级相关性；
• 当等于-1时，表示两个变量拥有完全相反的等级相关性；
• 当等于0时，两个变量相互独立。

下表给出了UV分别与PV、活跃用户数、新增内容用户数的三种相关性度量：

指标	Pearson相关系数	Spearman相关系数	Kendall相关系数
PV	0.85684	0.95513	0.84884
活跃用户数	0.88462	0.94131	0.83403
新增内容用户数	0.32988	0.38259	0.25761

可以发现：三种度量在这三对变量上没有明显的优劣；PV、活跃用户数都与UV成正向相关，且新增内容用户数与UV没有明显的相关性——这一点在变量的散点图中可以得到印证。

2. 参考资料

[1] 樊嵘, 孟大志, and 徐大舜. "统计相关性分析方法研究进展." 数学建模及其应用 3.1(2014).

[2] 王鹏, .